Qunfei@Data, ML and AI Architecture

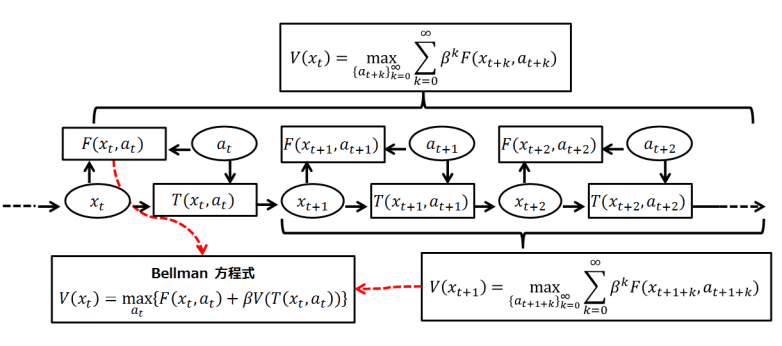
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming.^[1] It writes the “value” of a decision problem at a certain point in time in terms of the payoff from some initial choices and the “value” of the remaining decision problem that results from those initial choices.^{[citation needed]} This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman’s “principle of optimality” prescribes.^[2]

https://en.wikipedia.org/wiki/Bellman_equation

In English understanding，

1. Identify the Subproblems/Subphase in Time or Space
2. clearly express the recurrence relation with sub problems
3. Identify variables of states
4. State transition equation (Bellman_equation)
5. Define optimisation value Function/Lost function with boundary

In Chinese understanding,

1. 识别问题的多阶段性特征
2. 将问题分解成递推关系式联系起来的若干个子阶段
3. 正确的状态变量
4. 正确的定义状态转移方程
5. 找到最优的指标函数的递推关系及边界条件

In Programming understanding,

1. Define the state(s).
2. Define the recurrence relation(s).
3. List all the state(s) transitions with their respective conditions.
4. Define the base case(s).
5. Implement a naive recursive solution.
6. Optimize the recursive solution to caching (memoization).
7. Remove the overhead of recursion with a bottom-up approach (tabulation).

But the difficulties is in applying in real problem.